Introduction#
In a sequence of blog posts, I will try to explain the result of Burkland on multiplicative Moore spectra. Recently, I attended a seminar at NCMW, IIT Roorkee, where a series of talks on this topic was given by Prof. Samik Basu. This blog is based on my understanding of those talks and the paper by Burkland.
We begin with a simple analogy between algebra and stable homotopy theory: $$ (\mathbf{Sp}, \wedge, \mathbb{S}) \qquad \text{and} \qquad (\mathrm{Ab}, \otimes, \mathbb{Z}). $$
The Moore spectrum $\mathbb{S}/p$ is often viewed as an analogue of $\mathbb{Z}/p$, but this analogy is far from perfect. For example, while $$ \mathbb{Z}/m \otimes \mathbb{Z}/n \cong \mathbb{Z}/N $$ for a suitable integer $N$, no analogous formula holds for Moore spectra.
Rather than focusing on such tensor product behavior, we ask a more fundamental question: how similar are $\mathbb{Z}/p$ and $\mathbb{S}/p$ as multiplicative objects? The ring $\mathbb{Z}/p$ is associative and commutative, so one may ask whether $\mathbb{S}/p$ admits a multiplication, and if so, whether it can be made associative or commutative as a ring spectrum.
Theorem: $\mathbb{S}/2$ does not admit any unital multiplication.
Proof. Suppose that $\mathbb{S}/2$ admits a unital multiplication $$ \mu \colon \mathbb{S}/2 \wedge \mathbb{S}/2 \to \mathbb{S}/2. $$ Then the unit induces an equivalence $$ \mathbb{S}/2 \wedge \mathbb{S}/2 \simeq \mathbb{S}/2 \vee \Sigma \mathbb{S}/2. $$
However, in the cohomology of $\mathbb{S}/2$, the degree $0$ and degree $1$ classes are related by a Bockstein homomorphism. Consequently, $\mathbb{S}/2 \wedge \mathbb{S}/2$ admits a nontrivial Steenrod square operation $Sq^2$. Such an operation cannot exist on a wedge of suspensions of $\mathbb{S}/2$, yielding a contradiction. $\square$
It is also known that $\mathbb{S}/3$ admits neither a commutative nor an associative multiplication. Before motivating Burkland’s result, we recall some basic constructions.
Let $R$ be a ring spectrum and let $X$ be a spectrum equipped with a map $$ x \colon X \to R. $$ We define $R/x$ to be the cofiber of the composite $$\mu\circ (x \wedge 1): X\wedge R \to R \wedge R \to R$$ Given elements $x_1, \dots, x_n$, define $$ R/(x_1, \dots, x_n)=R/x_1 \wedge_R R/x_2 \wedge_R \cdots \wedge_R R/x_n. $$
A result in EKMM shows that if $R$ is an even ring spectrum and each $x_i$ lies in $\pi_{2k_i}(R)$, then $R/(x_1, \cdots, x_n)$ admits an $A_{\infty}$-ring structure. Since $\mathbb{S}/p$ does not admit an $A_{\infty}$-ring structure, this led Mahowald to conjecture that $\mathbb{S}/a$ is not an $A_{\infty}$-ring spectrum for any $a \in \pi_*(\mathbb{S})$.
Burkland disproved this conjecture by showing that $\mathbb{S}/p^2$ is an $A_{\infty}$-ring spectrum for all primes $p > 3$, and that $\mathbb{S}/2^3$ admits an $A_{\infty}$-ring structure, in fact an $\mathbb{E}_1$-ring structure.
In this series of blog posts, we will focus on the case of $\mathbb{S}/2^3$.
Towards the Sketch#
Let $E$ be an Adams-type spectrum. There is a notion of the synthetic homotopy category over $E$, denoted by $\mathbf{Syn}_E$. To understand the main proof we have to understand the following diagram of $\infty$-categories.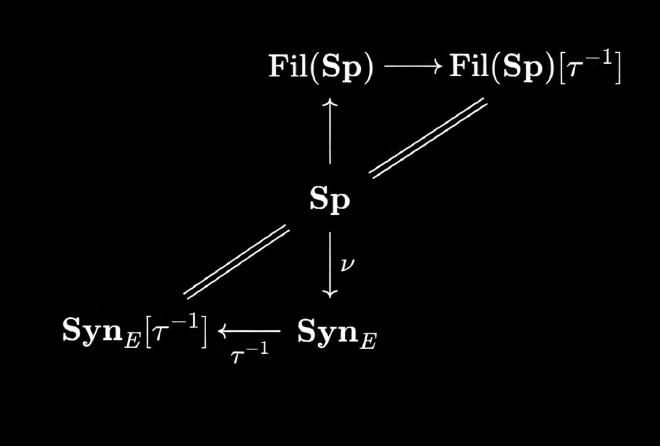
Once we have understanding of how to go back and forward across these homotopy theories we can provide the outline of the proof. We study, $$\nu(\mathbb{S}) / \tilde{2}^3\in\mathbf{Syn}_{HF}$$
where $\tilde{2}$ denotes the lift of $2$ in $\nu(\mathbb{S})_*$.
The key point is that this object admits an $\mathbb{E}_1$-ring structure in the synthetic category. After inverting the element $\tau$, this structure descends to give the desired multiplicative structure on $\mathbb{S}/2^3$.
